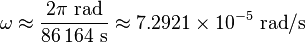In any circular orbit, the
centripetal force required to maintain the orbit is provided by the gravitational force on the satellite. To calculate the geostationary orbit altitude, one begins with this equivalence, and uses the fact that the orbital period is one
sidereal day.
By
Newton's second law of motion, we can replace the forces
F with the
mass m of the object multiplied by the
acceleration felt by the object due to that force:
We note that the mass of the satellite
m appears on both sides — geostationary orbit is independent of the mass of the satellite.[SUP]
[4][/SUP] So calculating the altitude simplifies into calculating the point where the magnitudes of the
centripetal acceleration required for orbital motion and the
gravitational acceleration provided by Earth's gravity are equal.
The
centripetal acceleration's magnitude is:
where
? is the
angular speed, and
r is the orbital radius as measured from the Earth's center of mass.
The magnitude of the
gravitational acceleration is:
where
M is the mass of Earth, 5.9736 × 10[SUP]
24[/SUP] kg, and
G is the
gravitational constant, 6.67428 ± 0.00067 × 10[SUP]
?11[/SUP] m[SUP]
3[/SUP] kg[SUP]
?1[/SUP] s[SUP]
?2[/SUP].
Equating the two accelerations gives:
The product
GM is known with much greater precision than either factor alone; it is known as the
geocentric gravitational constant ? = 398,600.4418 ± 0.0008 km[SUP]
3[/SUP] s[SUP]
?2[/SUP]:
The angular speed
? is found by dividing the angle travelled in one revolution (360° = 2? rad) by the orbital period (the time it takes to make one full revolution: one
sidereal day, or 86,164.09054 seconds).[SUP]
[5][/SUP] This gives:
The resulting orbital radius is 42,164 kilometres (26,199 mi). Subtracting the
Earth's equatorial radius, 6,378 kilometres (3,963 mi), gives the altitude of
35,786 kilometres (22,236 mi).
Orbital speed (how fast the satellite is moving through space) is calculated by multiplying the angular speed by the orbital radius:
To put it simply REAL FAST